HMM-CRF是做序列标注任务的标准算法之一。
预备知识
EM算法
期望最大化算法(Expectation-maximization algorithm,EM)是在概率模型中迭代求解参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。主要分为两个步骤:
- E步:计算期望值,利用对隐藏变量的现有估计值,计算其最大似然估计值;
- M步:期望最大化,最大化在E步上求得的最大似然值来计算参数的值。
M步上找到的参数估计值被用于下一个E步计算中,迭代更新隐含数据和模型分布参数,直到收敛,即得到所需模型参数。
要解决的问题
若要从样本观察数据中,找出样本的模型参数,最常用的方法就是极大化模型分布的对数似然函数。但若存在不可观察的隐含数据,因而无法直接用极大化对数似然函数得到模型分布的参数。这就是EM算法可以派上用场的地方了。
EM算法解决问题的思路是使用启发式的迭代方法,既然无法直接求出模型分布参数,那么先猜想隐含数据(E步),接着基于观察数据和猜测的隐含数据一起来极大化对数似然,求解模型参数(M步)。由于隐藏数据是猜测的,所以此时得到的模型参数距离想要的结果还有差距,不过只要不断的迭代下去,直到模型分布参数基本无变化,就可以找到合适的模型参数。
收敛性
1) EM算法能保证收敛吗?2) EM算法如果收敛,那么能保证收敛到全局最大值吗?
生成式模型与判别式模型
在监督学习下,模型可以分为判别式模型与生成式模型。下图可见,NB在序列建模下拓展到了HMM;LR在序列建模下拓展到了CRF:
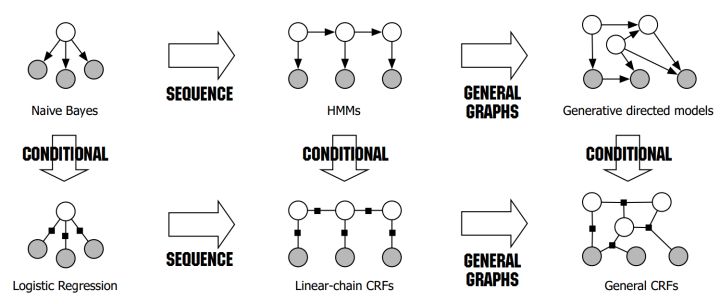
判别式模型
判别式模型从数据的标签和提供的特征直接学习建模,通过函数映射等学习,最后得到比较明显可以切分标签的边界,如线性LR、线性SVM。 更准确地说,判别模型是直接对$P(Y|X)$建模,也就是直接根据X特征来对Y建模训练,确定$P(Y|X)$模型的参数。
判别式模型特征有:
- 对 $P(Y|X)$ 建模;
- 对所有的样本只构建一个模型,确认总体判别边界;
- 观测到输入什么特征,就预测最可能的标签。
优点:对数据量要求没生成式的严格,速度也会快,小数据量下准确率也会好些。
生成式模型
生成式模型从训练样本数据中学习所有的数据分布情况,最终确定一个分布来作为所有的输入数据的分布,也就是所有的特征$x_i$和所有标签$y_i$的联合分布$P(X,Y)$ ,当进入推理过程时,通过条件概率公式$P(Y|X) = \frac{P(X,Y)}{P(X)}$,可以推断新样本的类别。具体说,训练阶段是只对$P(X,Y)$建模,需要确定维护这个联合概率分布的所有的信息参数,在推理阶段再对新的样本计算$P(Y|X)$,获得对应标签。
以朴素贝叶斯为例,学习阶段建模:$P(X,Y)=P(X|Y)P(Y)$,推理阶段$P(Y|X) = \frac{P(X,Y)}{P(X)}$。
生成式模型特征有:
- 对$P(X,Y)$建模;
- 对于分类问题,要对每个标签都需要建模,最终选择最优概率的标签为结果,所以没有判别边界;
- 中间生成联合分布,并可生成采样数据。
生成式模型的优点在于,所包含的信息非常齐全,不仅可以用来输入label,还可以干其他的事情。生成式模型关注结果是如何产生的。但是生成式模型需要非常充足的数据量以保证采样到了数据本来的面目,所以速度相比之下,慢。
马尔可夫假设
齐次马尔可夫假设:马尔可夫链 $x_1,⋯,x_n$里的$x_i$ 元素总是只受前一个元素$x_{i−1}$的影响,相当于2-gram。
马尔可夫过程:在一个过程中,每个状态的转移只依赖于前n个状态,并且只是个n阶的模型。
马尔可夫性:a. 成对,b. 局部,c. 全局。保证或者判断概率图是否为概率无向图的条件。
有向图与无向图
以一个经典的图模型衍生图为例:
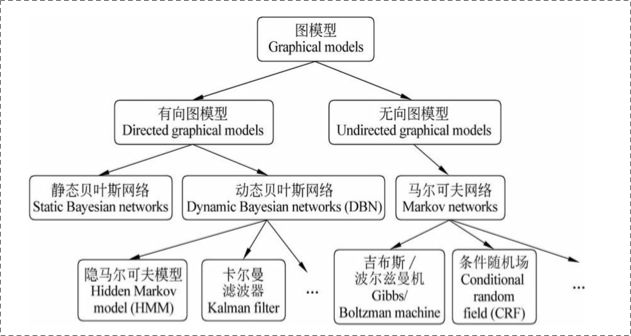
上图可以看到,贝叶斯网络都是有向的,马尔科夫网络无向。所以,贝叶斯网络适合为有单向依赖的数据建模,马尔科夫网络适合实体之间互相依赖的建模,其核心差异表现在如何表示$Y = ({y_1},…,{y_n})$这个的联合概率。
1. 有向图
有向图的每个节点对应一个随机变量,通过条件概率$P(x_i│Parents(x_i))$刻画父节点对$x_i$的影响,图中无回路,求联合概率有下列公式:$P({x_1},…,{x_n}) = \prod\limits_{i = 0} P({x_i}|\pi (x_i))$ 。
对于下面的有向图:
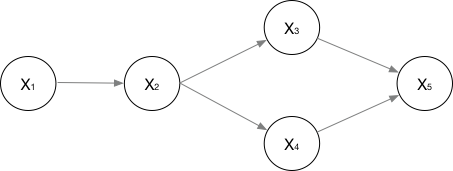
联合概率可以表示为:$P({x_1},…,{x_n}) = P({x_1})P({x_2}|{x_1})P({x_3}|{x_2})P({x_4}|{x_2})P({x_5}|{x_3},{x_4})$。
2. 无向图
无向图的每个节点也对应一个随机变量,每条边表示随机变量之间的依赖关系,联合概率分布满足局部马尔科夫性。一般的图结构如下所示:
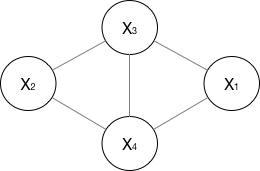
定义最大团的概念:无向图中任何两个结点均有边连接的结点子集称为团。如果无向图C是一个团,并且不能再加进任何一个结点使其成为更大的团,则称C为最大团。如上图$X_1,X_3,X_4$和$X_2,X_3,X_4$分别是两个最大团,而$X_1,X_2,X_3,X_4$并不是最大团,因为$X_1$和$X_2$没有连线。
所以对于一个无向图,可以将联合概率写为若干个最大团联合概率的乘积,有:$P(Y) = \frac{1}{Z(x)}\prod _{c} \psi _{c} (Y_c)$,其中$Z(x) = \sum\nolimits_Y {\prod\nolimits_c {{\psi _c}(Y_c)}}$,归一化处理;${\psi _c}({Y_c})$表示最大团C上随机变量的联合概率,也称作势函数。
上图可以表示为:$P(Y) = \frac{1}{{Z(x)}}({\psi _1}(X_1,X_3,X_4) \cdot {\psi _2}(X_2,X_3,X_4))$。
HMM算法
常规的序列数据一般用马尔科夫模型就可以表达,但实际使用HMM的场景是每个节点$X_i$下还附带着另一个节点$Y_i$ ,也就是隐含马尔科夫模型,那么除了可见的节点,还要将隐含状态节点一起建模。所以对于HMM,将$X_i$、$Y_i$ 换成$i_i$、$o_i$ ,名称变为状态节点和观测节点,其中状态节点就是隐状态,如下图所示:
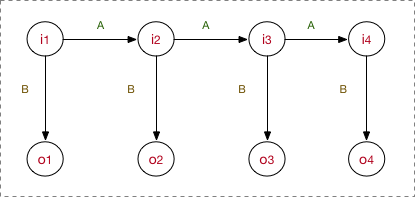
HMM属于有向图,是典型的生成式模型,要从训练数据中学到数据的各种分布,正是HMM的5要素,其中有3个就是整个数据的不同角度的概率分布:
- $N$:隐藏状态集$N = {{q_1},…,{q_N}}$,包含所有隐藏节点的状态;
- $M$:观测集$M = { {v_1},…,{v_M}}$,包含所有观测节点的状态;
- $A$:状态转移概率矩阵,$A = [a_{ij}]{N \times N}$,N是隐状态数量,$a{ij} = P(i_{t + 1}|i_t)$,$i_t$就是第t个隐状态节点,也就是遵循齐次马尔科夫链假设;
- $B$:观测概率矩阵,$B = [b_{ij}]{N \times M}$,N是隐状态数量,M是观测状态数量,$b{ij} = P(o_t|i_t)$,$o_t$是第t个观测节点,$i_t$就是第t个隐状态节点,意味着o对i有依赖性,也就是观测独立性假设;
- $\pi$:初始状态概率分布,为第一个隐状态$i_t$分配概率。
在学习过程中,HMM会确定以上5要素,在推理过程:隐状态节点$i_t$是不能直接观测到的数据节点,$o_t$才是能观测到的节点,并且注意箭头的指向表示了依赖生成条件关系,$i_t$在$A$的指导下生成下一个隐状态节点$i_{t+1}$,并且$i_t$在$B$的指导下生成依赖于该$i_t$的观测节点$o_t$。
以序列标注任务,实体识别为例,所有文本里的token构成的列表是观测集M ,因为token序列在推理阶段是可见的;标注集BIEOS构成隐藏状态集N,这是模型的预测任务;至于A、B、$\pi$的概率分布信息是在学习过程中确定的参数。
模型参数学习过程
HMM学习训练的过程,就是给定观测序列$O={o_1,o_2,…o_T}$,找出数据的分布情况,也就是模型参数A,B和$\pi$的确定,使观测序列的条件概率最大。学习算法主要有以下两种:
- 在有隐状态序列的情况下,使用极大似然估计;
- 在没有隐状态序列的情况下,使用Baum-Welch(前向后向)算法。
1. 极大似然估计
一般做NLP的序列标注等任务,在训练阶段肯定是有隐状态序列的,步骤很简单:
- 计算A:$a_{ij} = \frac{A_{ij}}{\sum_{j = 1}^N A_{ij}}$;
- 计算B:$b_j = \frac{{B_{jk}}}{\sum\nolimits_{k = 1}^M {B_{jk}}}$;
- 最后估计$\pi$。
2. Baum-Welch(前向后向)
Baum-Welch是一个EM的过程,步骤如下:
- 随机初始化所有的A,B,$\pi$;
- 对于每个样本,使用前向后向算法计算联合概率分布;
- 更新模型参数,若参数没有收敛,返回2继续迭代。
预测(解码)过程
对于预测过程,就是给定模型参数A,B,$\pi$和观测序列$O={o_1,o_2,…o_T}$,求给定观测序列条件下,最可能出现的对应的隐状态序列,也就是已知了$P(Q,O)$,现在要求出$P(Q|O)$,即$Q_{max} = \arg {\max _{allQ}}\frac{P(Q,O)}{P(O)}$。
使用的算法是维特比算法,在HMM中维特比算法定义了两个局部状态用于递推。第一个局部状态是在时刻t隐藏状态为i所有可能的状态转移路径$i_1,i_2,…,i_t$中的概率最大值,第二个局部状态由第一个局部状态递推得到。
评估观测序列概率
评估观测序列概率就是给定模型参数$\lambda=(A,B,\pi)$和观测序列$O={o_1,o_2,…o_T}$,求给定模型下观测序列条件出现的概率$P(O|\lambda)$。
主要的计算有三类算法:1. 直接计算法(穷举搜索);2. 前向算法(DP);3. 后向算法(DP)
MEMM
MEMM,即最大熵马尔科夫模型,属于判别式模型,直接为了确定边界使用后验概率建模。
在HMM中,观测节点$o_i$依赖隐藏状态节点$i_i$。但在更多的实际场景下,观测序列是需要很多的特征来刻画的,而MEMM模型则允许直接定义特征,学习条件概率$P(i_t|{i_{t - 1}},o_t)(t = 1,…,n)$,这个概率通过最大熵分类器建模,得到: $$ P(i|i’,o) = \frac{1}{Z(o,i’)}\exp (\sum\nolimits_a {\lambda _a{f_a}(o,i)} ) $$ 其中$Z(o,i’)$表示归一化,${f_a(o,i)}$是特征函数,需要手动定义,$\lambda$是特征函数的权重,需要从训练中学习得到。
MEMM需要注意:
- 与HMM的$o_t$依赖$i_t$不一样,MEMM当前隐藏状态$i_t$依赖当前时刻的观测节点$o_t$和上一时刻的隐藏节点$i_{t−1}$;
- 图的箭头方向,是由MEMM的公式决定的,公式是手动定义的。
可以得到流程图:
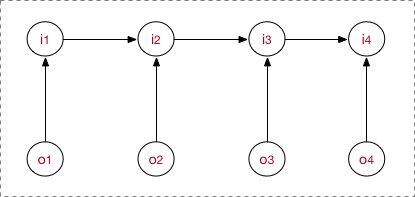
总结流程:
- 定义特征函数${f_a(o,i)}$;
- 训练模型,确定参数;
- 序列标注或者序列求概率。
参数学习训练过程
MEMM参数同样需要通过训练数据学习得到,有极大似然估计、梯度下降等方法。
序列标注过程
与HMM一致,用学习好的MEMM模型,在观测序列$o_1,⋯,o_t$上找出一条概率最大的隐状态序列$i_1,⋯,i_t$。路径求解过程也是采用维特比算法。
评估观测序列概率
与HMM一致,分别为每一批数据训练构建特定的MEMM,然后根据序列在每个MEMM模型的不同得分概率,选择最高分数的模型。
标注偏置问题
MEMM存在序列标注过程中的标注偏置问题。
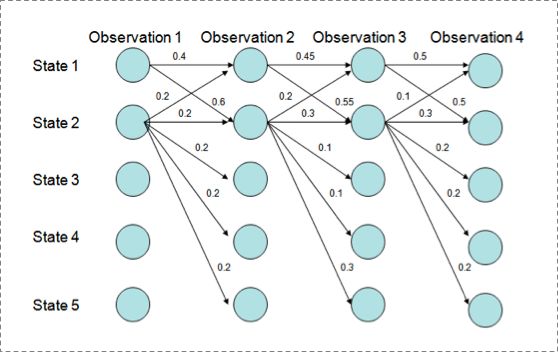
用维特比算法解码MEMM,状态1倾向于转换到状态2,同时状态2倾向于保留在状态2:
- $P(1 \to 1 \to 1 \to 1) = 0.4 \times 0.45 \times 0.5 = 0.09$
- $P(2 \to 2 \to 2 \to 2) = 0.2 \times 0.3 \times 0.3 = 0.018$
- $P(1 \to 2 \to 1 \to 2) = 0.6 \times 0.2 \times 0.5 = 0.06$
- $P(1 \to 1 \to 2 \to 2) = 0.4 \times 0.55 \times 0.3 = 0.066$
但得到的最优的状态转换路径是$1 \to 1 \to 1 \to 1$,因为状态2可以转换的状态比状态1要多,从而使转移概率降低。所以MEMM倾向于选择拥有更少转移的状态,以提高整体的后验概率。
由于MEMM的归一化过程在指数内部,所以属于局部归一化,而维特比求解过程中,使用的状态转移公式无法正确低轨道全局最优解。
CRF
一般情况下CRF专指线性链CRF(Linear chain CRF):
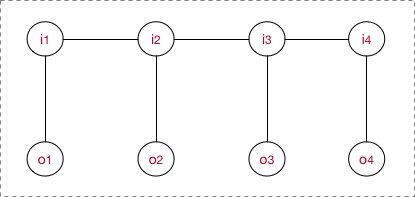
无向图的联合概率分布可以分解为: $$ P(Y|X) = \frac{1}{Z(x)}\prod\nolimits_c e^{\sum\nolimits_k {\lambda k}f_k (c,y|c,x)} = \frac{1}{Z(x)} e^{\sum\nolimits_c \sum\nolimits_k {\lambda k}f_k (y_i,y{i - 1},x,i)} $$ 在线性链CRF中,每一个I-O对都是一个最大团,且满足$P({I_i}|O,{I_1},…,{I_n}) = P({I_i}|O,{I{i - 1}},{I_{i + 1}})$。
因此CRF建模公式为: $$ P(Y|X) = \frac{1}{Z(x)} e^{\sum\nolimits_c \sum\nolimits_k \lambda k f_k (y_i,y{i - 1},x,i)} = \frac{1}{Z(O)} e^{\sum\nolimits_i^T \sum\nolimits_k^M \lambda k f_k (O,I{i - 1},I_i,i)} $$ 其中下标i表示当前所在节点位置;k表示第几个特征函数,每个特征函数都有权重$\lambda _k$,也就是每个团里面为每个token构造M个特征,建模时为每个特征函数加权求和;$Z(O)$表示归一化,形成概率值;
CRF特征函数:$\sum\nolimits_i^T \sum\nolimits_k^M {\lambda k}f_k(O,I{i - 1},I_i,i) $,为每个token打分,最后将所有分数进行log linear表示,求和后归一化就可以得到概率值。
模型的工作流程以及三个任务同MEMM一致。
LSTM+CRF
LSTM和CRF都可以预测token的标签,但是预测机理是不同的。CRF是全局范围内统计归一化的条件状态转移概率矩阵,再预测出一条指定的sample的每个token的label;LSTM是依靠神经网络的超强非线性拟合能力,在训练时将特征通过高维空间的非线性变换,学习出一个模型,然后再使用softmax预测出每个token的标签。
LSTM存在标注错误问题,如:
- 输入:学习出一个模型
- 期望输出:学/B习/E 出/S 一/B个/E模/B型/E
- LSTM输出:学/E习/E 出/S 一/B个/B模/B型/E
因为softmax只做了局部的考虑,没有考虑前后词之间标签的关系,上述错误在CRF中是不存在的,因为CRF的特征函数就是为了观察学习各种特征,也就是限定窗口下的各种词之间的关系,如:开头是E,B后面接E,不会出现B。这个限定特征会使得CRF的预测结果不出现上述例子的错误。
在LSTM+CRF中,CRF的特征分数直接来源于LSTM传上来的隐状态的值;而在经典CRF中,分数是统计来的。隐状态本身当做特征分数形成转移矩阵再让viterbi进行路径搜索,这就是CRF的意义。
对比
- HMM -> MEMM: HMM模型中存在两个假设:(1)观测值之间严格独立;(2)齐次马尔科夫假设,状态的转移过程中当前状态只与前一状态有关。但实际上序列标注问题不仅和单个词相关,而且和观察序列的长度,单词的上下文等相关。MEMM解决了HMM观测独立性假设的问题。因为HMM只限定在了观测与状态之间的依赖,而MEMM引入自定义特征函数,不仅可以表达观测之间的依赖,还可表示当前观测与前后多个状态之间的复杂依赖。
- MEMM -> CRF:(1)CRF不仅解决了HMM输出独立性假设的问题,还解决了MEMM的标注偏置问题,MEMM容易陷入局部最优是因为只在局部做归一化,而CRF统计了全局概率,在做归一化时考虑了数据在全局的分布,而不是仅仅在局部归一化,这样就解决了MEMM中的标记偏置的问题,使得序列标注的解码变得最优解。(2)HMM、MEMM属于有向图,所以考虑了x与y的影响,但没把x当做整体考虑进去(这点问题应该只有HMM),CRF打破了HMM 的齐次马尔科夫假设,属于无向图,没有这种依赖性,克服此问题。