使用self-attention的经典模型Transformer，和基于其Encoder结构的预训练模型Bert，为NLP领域开创了新时代。

Transformer

Transformer是在Attention is All You Need提出的的模型框架，用于解决序列转写任务。这里借用经典的图做一下解释：

img

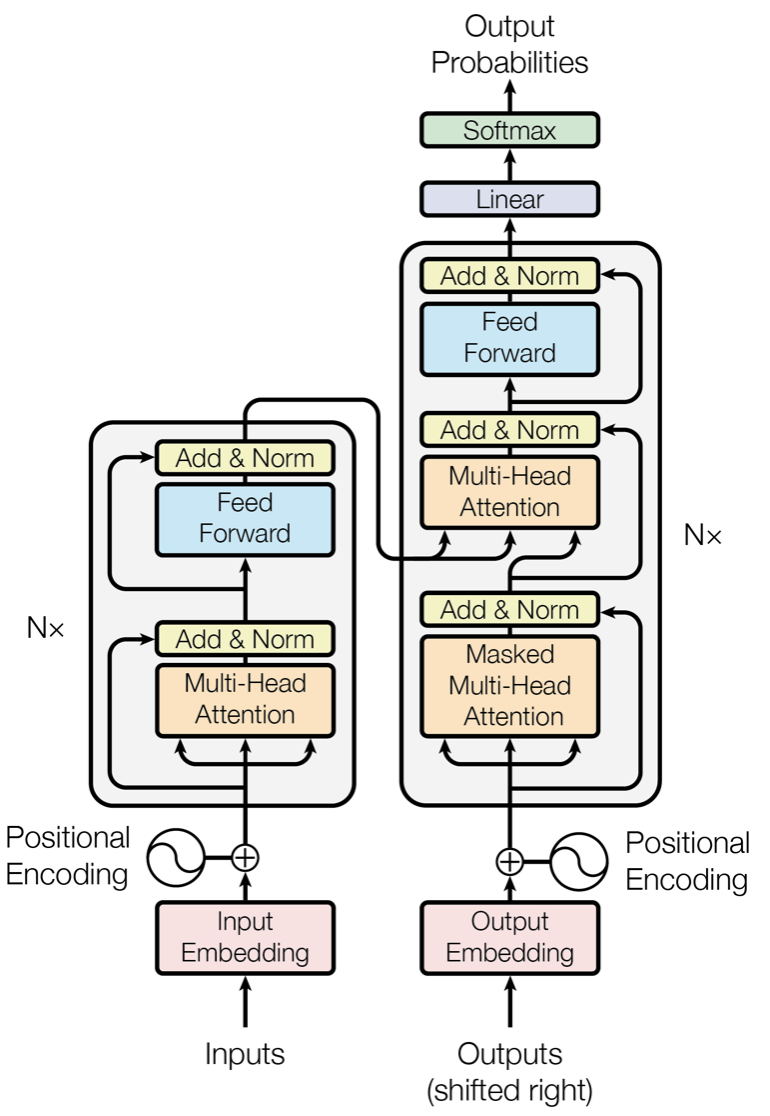
Transformer遵循Encoder-Decoder结构，上图左侧Inputs部分为Encoder，右侧Outputs部分为Decoder，两者均为多个Transformer Block堆叠而成，但Encoder的Transformer与Decoder的Transformer是有略微区别的：

  • Encoder端使用的attention不需要masked，而Decoder需要Masked；
  • Decoder中多了一层Encoder-Decoder attention，其中的Query是self-attention 计算出的上一时间i处的编码值，Key和Value都是Encoder的输出。
Embedding

Embedding是transformer的基础，文本需要转换为embedding，才可送入Encoder做后续运算。Transformer的Embedding包括两个部分，一个是Word embedding，另一个是Positional embedding。

Word Embedding

与传统Word Embedding技术一致，通过查表方式，根据token的id将token转为embedding。

Positional Embedding

由于Attention采用的并行计算，导致token的计算逻辑，不具备任何的位置信息，次序打乱之后也不会影响attention的计算结果，所以必须引入位置向量，确保位置信息不会被丢弃。在Transformers中，位置信息使用的绝对位置，构造位置编码的公式如下所示： $$ \left{ {\begin{array}{*{20}{c}} {P{E_{2i}}(p) = \sin (p/{{10000}^{2i/{d_{pos}}}})}\ {P{E_{2i + 1}}(p) = \cos (p/{{10000}^{2i/{d_{pos}}}})} \end{array}} \right. $$

对不同维度使用不同频率的正/余弦公式进而生成不同位置的高维位置编码，利用正余弦函数实现相对位置信息的表示。

为什么奇偶维度之间需要作出区分，分别使用 sin 和 cos 呢？奇偶区分可以通过全连接层帮助重排坐标，所以可以直接简单地分为两段(前 256 维使用 sin，后 256 维使用 cos)。

组合方法

词向量和位置向量二者直接对应相加，得到最终的向量嵌入。

这样操作是否会影响到原始的输入特征呢？根据johnson–lindenstrauss 定理：通俗的理解是两个高维的向量总是近似正交的，可以认为无论是add还是concat，两个向量耦合性小，丢失的信息量少，因为维度足够高，所以即使有部分信息被正余弦信号遮蔽，仍然有足够的特征可以用来辨识。

Encoder

从Encoder段开始介绍，由上图可知，一个Encoder块主要由两部分组成：多头注意力机制(Multi-Head Attention)和前馈神经网络(Feed Forward)，二者都通过残差结构连接。

多头注意力机制

多头注意力模块结构如下图所示：

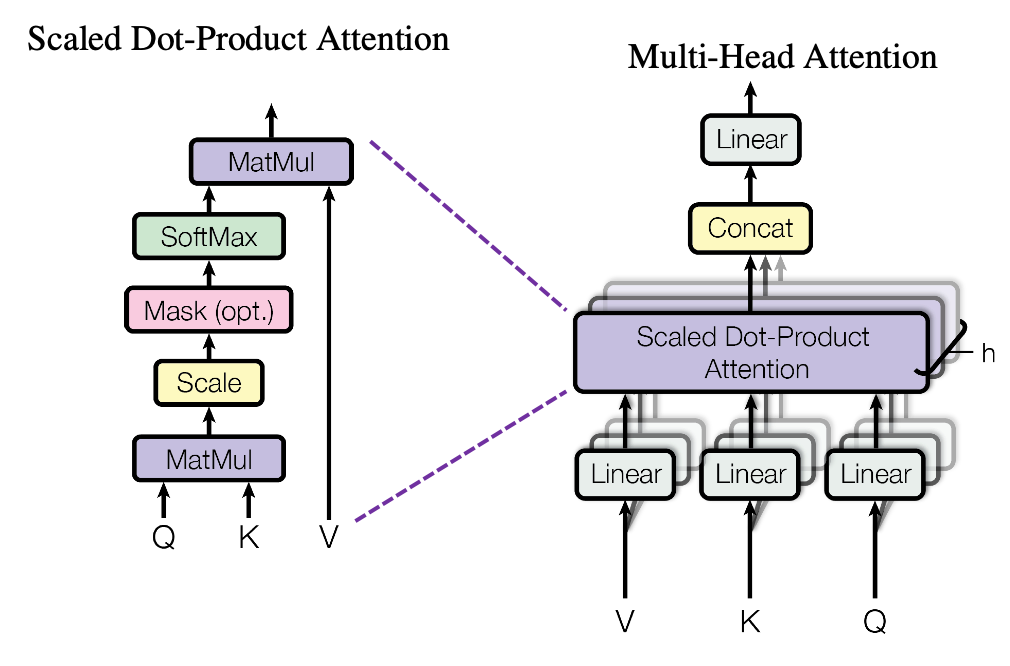img 这里可以看出整个模块是由h个Scaled Dot-Product Attention模块堆叠而成的，可以类比CNN中同时使用多个卷积核的作用，有助于捕捉到更丰富的特征信息。主要步骤如下：

  1. 向量生成：将token的embedding经过线性变换，生成Q、K、V三个向量；
  2. Attention切分：将Attention按照指定的head数量切分，如512维度分成8个head，每个head维度为64；
  3. Self Attention计算：对每个head进行Scaled Self Attention计算；
  4. 连接：对于h个Scaled Self Attention的输出，进行简单的拼接，并通过与一个线性映射矩阵${W_o}$与其相乘（目的是对输出矩阵进行压缩），从而得到整个Multi-Head Attention的输出。

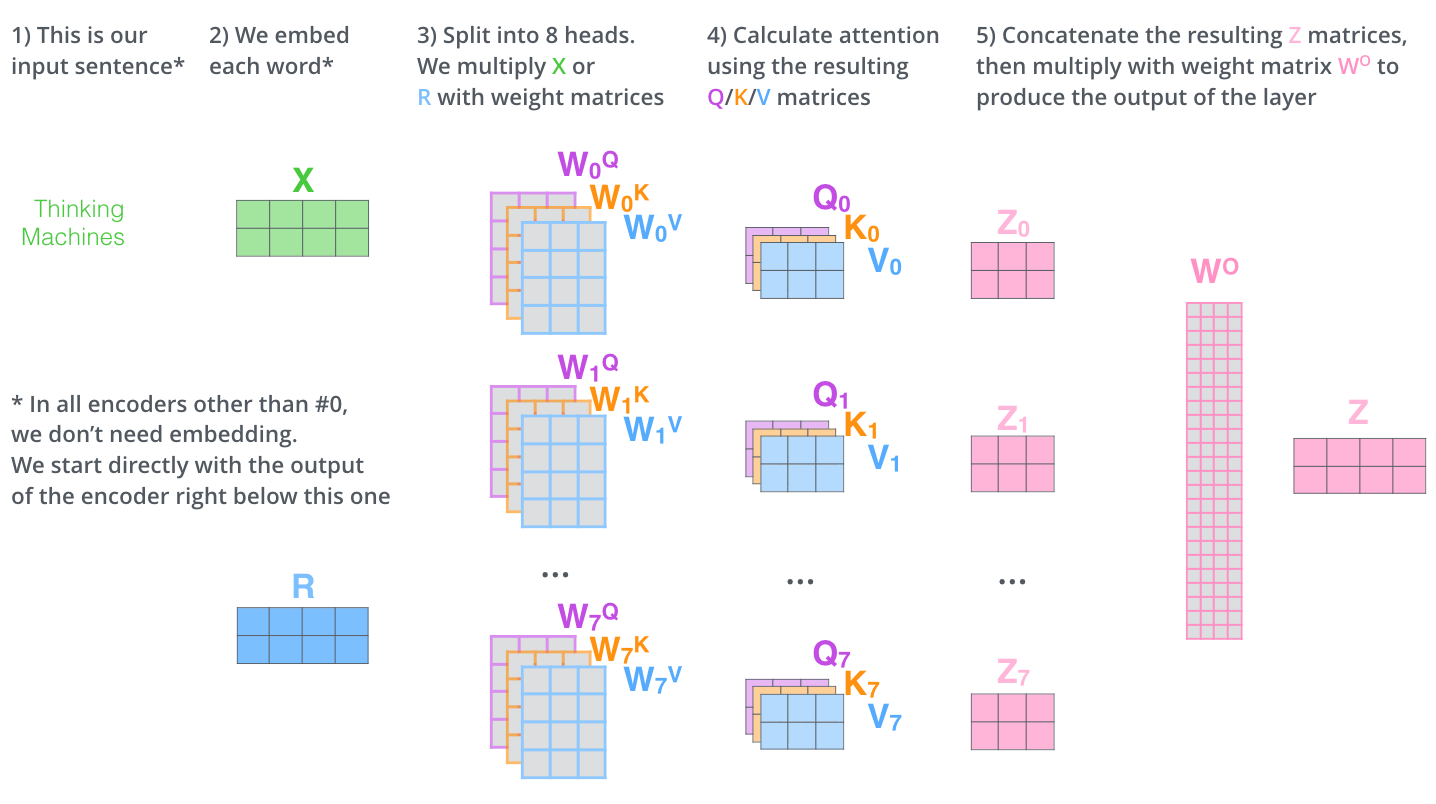
下图是一个简单的multi-head attention计算过程：

  1. 输入句子 Thinking Machines;
  2. 将原句Tokenizer后转成Word Embedding X，假设维度512；
  3. 假设头的个数为8个，将Embedding X切分为8份，每份维度64，并将其分别赋予key、query、value，每个都乘以对应权重矩阵$w_i^k$，$w_i^q$，$w_i^v$，得到输入向量$K_i$，$Q_i$，$V_i$；
  4. 8个头分别计算Attention矩阵，${Z_i} = soft\max (\frac{{{Q_i}K_i^T}}{\sqrt {{d_k}}}){V_i}$；
  5. concat拼接融合8个头的结果${Z_i}$，点乘权重$W_o$得到最终输出Z。

img

在Multi-Head Attention中，最关键的部分就是Self-Attention部分了，也就是上图所说的Scaled Dot-Product Attention，计算过程可以用以下的矩阵形式进行并行计算: $$ Attention(Q,K,V) = softmax (\frac{{Q{K^T}}}{{\sqrt {{d_k}} }})V $$ 其中，Q, V, K分别表示输入句子的Queries, Keys, Values矩阵，矩阵的每一行为每一个词对应的向量Query, Key, Value向量，$d_k$表示向量长度。也正是因此，Transformer具有RNN所缺失的并行计算能力。

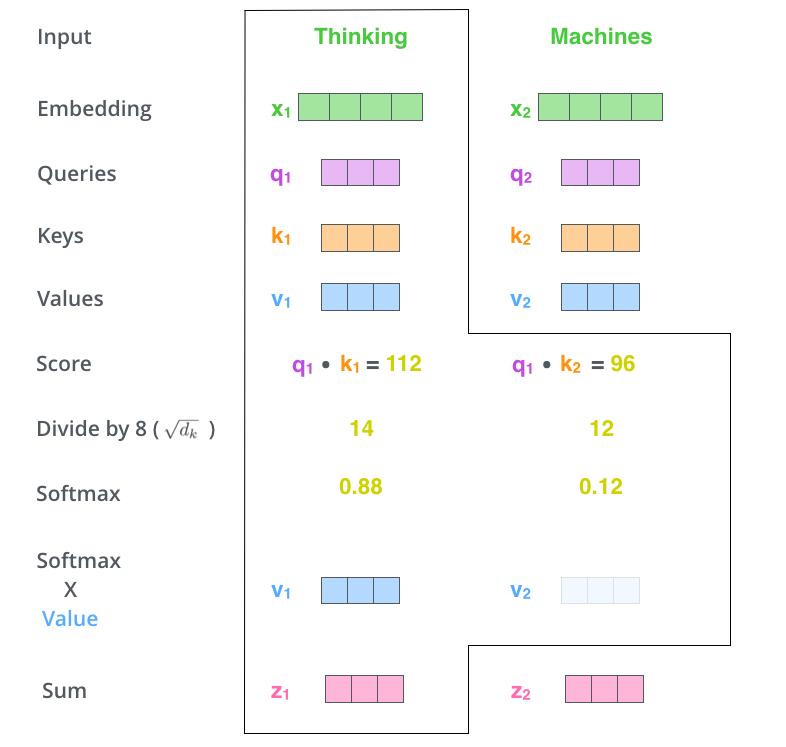
依旧以Thinking Machines为例，下图给出了两词计算self-attention计算的过程：

  1. 首先对每个输入单词向量Embedding X生成三个对应的向量：Query，Key 和 Value。这三个向量相比于向量X要小的多，因为每一个都会被拆分成headnum个独自计算，并且最后这headnum个输出会拼接恢复成原维度向量；
  2. 用Queries和Keys的点积计算所有单词相对于当前词(图中为Thinking)的权重得分，该分数决定在编码单词Thinking时其他单词给予的权重贡献度调整；
  3. 将Score除以向量维度64的平方根，再对其进行Softmax，将所有单词的分数进行归一化，这样对于每个单词都会获得所有单词对该单词编码的贡献分数，当然当前单词将获得最大分数，但也将会关注其他单词的贡献大小；
  4. 对得到的Softmax分数乘以每一个对应的Value向量；
  5. 对所得的所有加权向量求和，即得到Self-Attention对于当前词Thinking的输出。

img

Tips：

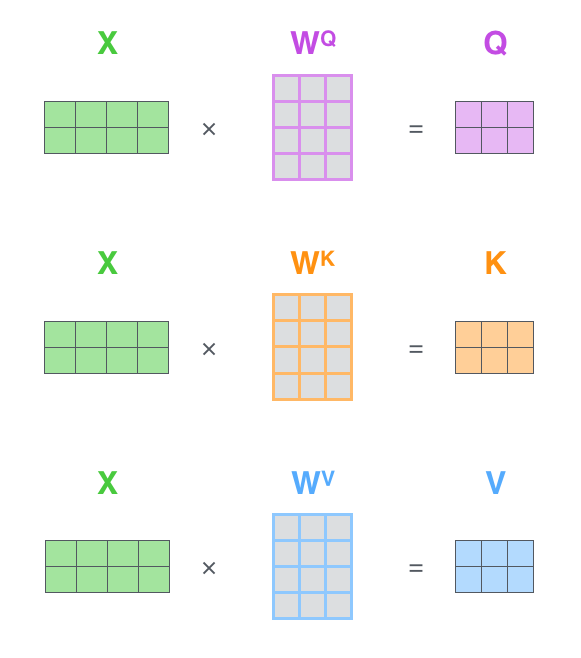
  1. KQV是怎么从token转换而来的？下面这个图可以给出结论，对于每个向量，都会维护一个映射矩阵，并且不同Self-Attention模块之间的权值不共享，将输入的矩阵X与三个映射矩阵相乘，得到三个输入Queries、Keys和Values。要注意这里的X可以是初始输入的token(也就是Input Embedding + Positional Embedding)也可以是上一层Transformer的输出。

img

  1. self-attention为什么要除以$\sqrt {{d_k}}$？

    • 首先，点积的目的是为了获得query和key的相似度，后续会接softmax进行计算，当query和key之间的方差过大时，softmax计算结果会出现非0即1的情况，会向很小的梯度的方向靠拢，训练效果不佳。而除以$\sqrt {{d_k}}$缩放了矩阵乘积范围，可以获得更加平滑的softmax结果，训练效果更好；

    • 假设Q和K是标准正态分布，均值为0，方差为1。它们的矩阵乘积将有均值为0，方差为 ${d_k}$ 。而$\sqrt {{d_k}}$用于缩放时，Q和K的矩阵乘积的均值为0，方差为1，可以获得一个更平缓的softmax。

$$ q \cdot k = \sum\nolimits_{i = 1}^{{d_k}} {{q_i}{k_i}} $$

  1. 为什么一定要定义kqv三个元素？

    注意力机制目的是要学习到一个权值，自注意力机制可以通过权重矩阵学习词与词之间的关系，但是如果只定义一个元素，无法分别表示自身与其他元素，其他元素与自身的权重，所以至少需要kq两个元素表示；而找到了权重之后，为了给原值加权，需要另外定义一层可以学习的参数，增强网络的学习能力。

    另外，如果只定义一个元素，那么很显然每个元素对于自己的注意力永远是最大的，挤压了其他的注意力得分，参数太少也影响模型容量。

    有解释是参考了Memory Network，用输入的query检索k-v memories，得到相似memory的key，计算相关性后对value进行加权求和。

    还有解释是对embedding矩阵起到降维，降低运算量的目的。

前馈神经网络

Transformers的前馈网络层很简单，由两个全连接层构成，第一层的激活函数为 ReLu，第二层不使用激活函数。在Bert代码中，Intermediate Layer作为FFN的第一层全连接层，其维度是（hidden_size，intermediate_size），且intermediate_size比hidden_size大很多，Output Layer作为第二层，不使用激活函数。

为什么要加入一层前馈神经网络呢？可以看出，多头Attention进行的主要是矩阵乘法，也就是说进行的全都是线性变换，也就是对权重的重新分配，而线性变换的学习能力不如非线性，尽管Attention机制学习到了每个词汇的表达，但是表达能力不强，需要通过激活函数强化表达能力（提供非线性映射，增强数据大的部分，抑制数据小的部分）。

在论文中对这一部分的解释是，可以将其视作两个具有$1\times1$卷积核的卷积神经网络，$1\times1$卷积核可以让每个位置进行独立运算，不需要关注周边信息，而中间扩增的结构类似于Resnet的bottleneck结构，减少计算量，增加网络的表示能力。

Layer Normalization

在每个Block中，无论是MHA还是FFN都添加了层间归一化模块，随着网络深度的增加，保证数据特征分布的稳定性，加入正则化，使用更大的学习率，加速模型的收敛速度。同时，正则化也有一定的抗过拟合作用，使训练过程更加平稳。

为什么Transformer使用LayerNorm ，而不使用BatchNorm？BN的特点是强行拉平数据之间的分布，使得模型收敛速度更快，并且起到了正则化的作用，使模型效果更佳。但是，BatchNorm对Batch Size大小很敏感，并且在LSTM网络上效果极差。LayerNorm是横向归一化，不受Batch Size大小的影响，并且可以很好地应用在时序数据中，而且不需要额外的储存空间。《Rethinking Batch Normalization in Transformers》一文对比了LayerNorm和BatchNorm对于Transformer的作用，并且提出了一种新的归一化方式。

残差模块(Residual Block)

残差模块是借鉴自CNN的思想，可以解决梯度消失和网络退化问题，构造更深的网络。 首先，残差模块能让训练变得更加简单，如果输入值和输出值的差值过小，那么可能梯度会过小，导致出现梯度小时的情况，残差网络的好处在于当残差为0时，改成神经元只是对前层进行一次线性堆叠，使得网络梯度不容易消失，性能不会下降。 其次，随着网络层数的增加，网络会发生退化现象：随着网络层数的增加训练集loss逐渐下降，然后趋于饱和，如果再增加网络深度的话，训练集loss反而会增大，注意这并不是过拟合，因为在过拟合中训练loss是一直减小的。 加入残差网络后，在前向传播时，输入信号可以从任意低层直接传播到高层。由于包含了一个天然的恒等映射，一定程度上可以解决网络退化问题。

Decoder

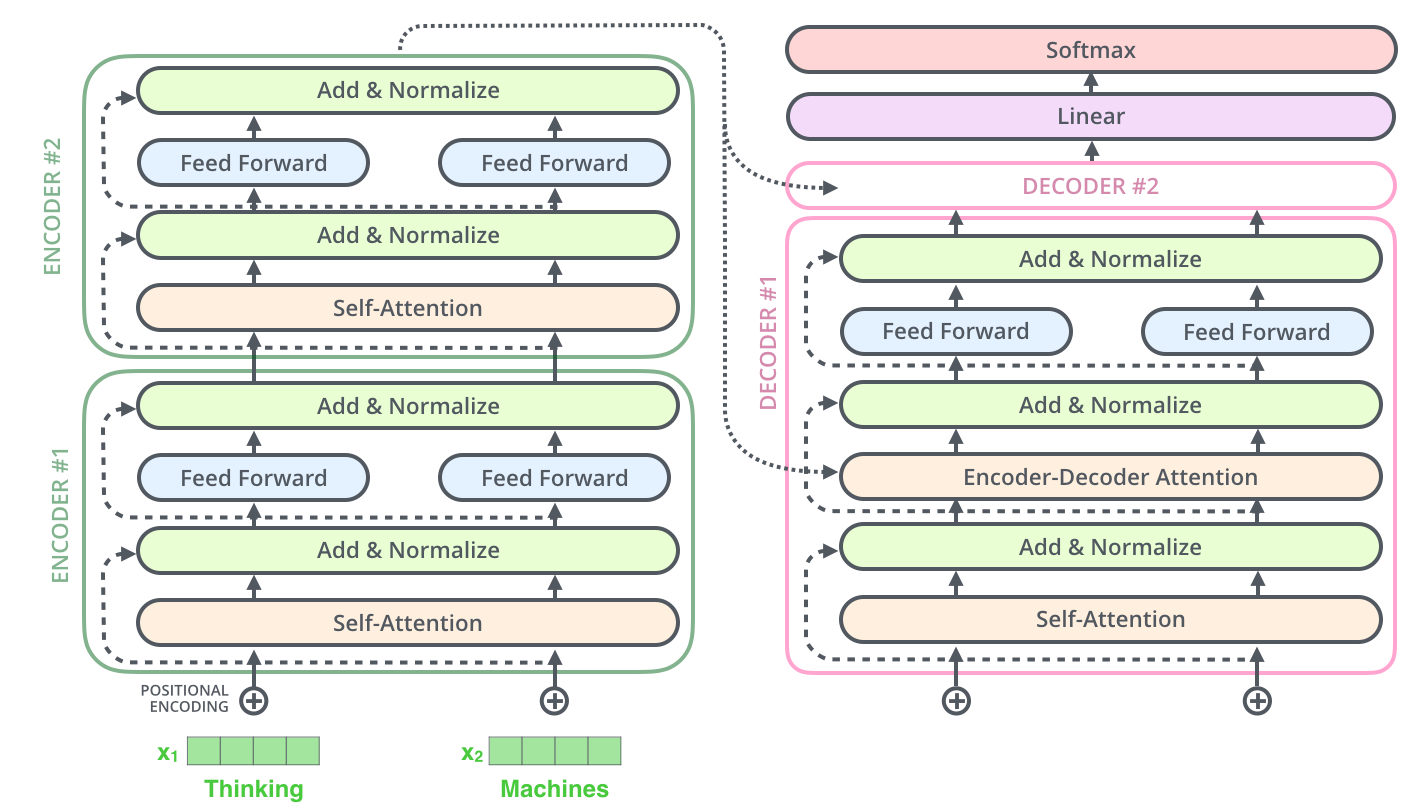
Transformer的Decoder端主要由三个模块构成，分别是Masked Multi-head attention、Encoder-decoder attention和Feed Forward Layer，除FFL外，另外两个Attention的结构与Encoder端的Attention结构也是一致的，只是在训练和预测阶段操作稍有不同。整体流程图如下所示：

img

Masked Multi-head attention

这一个Attention采用了Mask操作，因为在解码过程中，需要顺序进行，得到$i$个词之后，才可以进行$i+1$个词的预测，通过Mask操作可以防止第$i$个词看到后续词的信息。

需要注意，在Training过程中，需要Mask操作，而在Prediction过程中，无需Mask操作。

Decoder训练过程中可以使用Teacher forcing和并行化训练，Mask操作如下所示，一般做法是将需要被mask的向量设置为负无穷，那么经过点积和softmax之后其结果趋近于0，对最终结果也几乎没有任何影响，只对QK操作有影响：

img

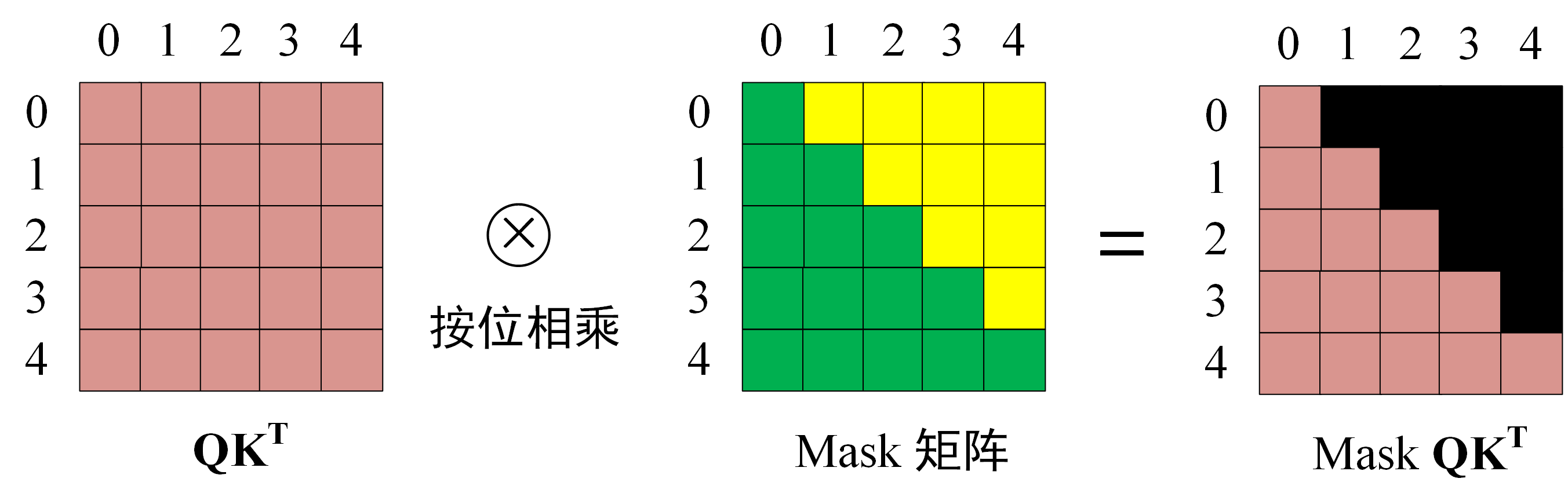
为什么在训练阶段可以并行化训练，因为已经知道了正确的译文，因此可以同时模拟已知前$i$ 个译文token情况下，训练decoder去预测第 $i+1$ 个译文token。

Encoder-decoder attention

这个部分的Attention的目的是建立Encoder和Decoder之间的关系，主要区别在与Attention的K，V矩阵不是来自上一个Decoder Block的输出，而是来自Encoder端的输出，但是Q矩阵还是来自于上一个Decoder Block的输出。

输出端

在最后一层Decoder Block后，接Linear将输出转为vocab_size长度，后接softmax算出最大概率logit输出。

Bert

结构

Bert是一种语言模型，使用的是Transformers的Encoder模块，并在embedding层添加了segment embeddings做NSP任务。

学习任务
  1. MLM任务，主要是预测掩码元素，在原文中15%的token被掩掉，其中80%的token使用[mask]替换，10%的token使用随机token替换，10%的token保持不变。mask太少会导致学习不充分，增加训练时长；mask太多会导致使一段文本中丢失太多的语义信息。（跟CBOW相似，15%相当于7个token预测一个token，刚刚好。）
  2. NSP任务：预测下一句话，是否是前一句话的下一句话。这个任务主要使用CLS的Embedding，它能否表示sentense embedding呢？从任务可见，pretrain的cls embedding很大程度上就是在编码NSP任务所需的高阶特征，也就是描述两段文本是否构成上下文关系，所以说，这个特征既然不是描述sentence语义的，直接用到sentence embedding上效果不好，但是finetuning之后可以获得不错的效果。
  3. BERT中的token mask方法对理解文本语义任务极有帮助，但这种方式具有硬伤：
    1. 预训练时输入句子带mask，而fine-tune不带，导致上下游任务不匹配问题。
    2. transformer的encoder的all attention结构，需要句子all token参与attention，这注定与自回归的NLG任务无法配套使用。
分词问题

词表的构建选用基于BPE算法的WordPiece算法，将通过频率合并字符的频率变成了通过语言模型的似然进行合并，其思想是选择能够提升语言模型概率最大的相邻子词加入词表。

BPE与Wordpiece都是首先初始化一个小词表，再根据一定准则将不同的子词合并。

BPE与Wordpiece的最大区别在于，如何选择两个子词进行合并：BPE选择频数最高的相邻子词合并，而WordPiece选择能够提升语言模型概率最大的相邻子词加入词表。

BasicTokenizer： 转unicode -> 去除空字符、替换字符、控制字符和空白字符等奇怪字符 -> 中文分词 -> 空格分词 -> 小写、去掉变音符号、标点分词；

WordpieceTokenizer：大致分词思路是贪婪最长优先匹配算法，按照从左到右的顺序，将一个词拆分成多个子词，每个子词尽可能长。

对中文：BERT 采取的是将每一个汉字都切开的策略。

Whole-word-mask策略：WordPiece构建的词表，会有很多子词，掩码时会导致信息不全。引入全词掩码，若一个word被切开，则全部切分的子词都要被掩掉。

可能的问题：

  • 词汇量不足：对于英文词汇，专有名词被拆分；
  • 拼写错误/缩写问题：拼写错误/缩写可能会导致模型性能大幅下降，subword导致切分与原文完全不一致；
  • 前缀问题：WordPiece 旨在处理后缀和简单的复合词，没有前缀的概念。

解决方法：

  • 超大规模预训练数据和模型结构；
  • 纠错，预处理删除无意义字符串，缩写扩充；
  • 分解复合词，将前缀视为复合词并将它们分开。

Quiz

  1. Bert模型的做句向量的缺陷：直接使用Bert做句向量的输出，会发现所有的句向量两两相似度都很高。因为对于句子来说，大多数的句子都是使用常见的词组成的，Bert的词向量空间是非凸的，大量的常见的词向量都是在0点附近，从而计算出的句子向量，都很相似。
  2. 如何解决Bert句向量的缺陷：使用双塔模型，将两个句子传入两个参数共享的Bert模型，将两个句向量做拼接，进行有监督的学习，从而调整Bert参数，此方法叫sentencebert；使用无监督或者有监督的对比学习，将同一个句子传入相同的bert(dropout = 0.3)得到标签为正例的一个句子对。通过这种方式来做Bert的微调整，得到SimCSE模型。

参考

  1. The Illustrated Transformer
  2. Transformers Explained Visually
  3. 深入理解Transformer模型